Cette page explique les règles du jeu du morpion en quatre dimensions et fournit un programme au format Excel permettant de jouer à deux ou contre l'ordinateur. Il est bien évidemment également possible de jouer avec une simple feuille de papier et un stylo.
Introduction
Le jeu de morpion sur une grille de $3 \times 3$ cases est bien connu mais très ennuyeux. Il est possible de complexifier le jeu en utilisant une grille plus grande: $10 \times 10$, $20 \times 20$... Mais pourquoi ne pas rendre le jeu encore plus attrayant en ajoutant des dimensions? Un morpion en trois dimensions est certainement bien plus marrant qu'en deux dimensions. Et tant qu'on y est, autant aller jusqu'à quatre dimensions, où la visualisation de la grille de jeu et des coups de l'adversaire devient assez acrobatique et fera surchauffer les cerveaux sensibles.
Règles du jeu
La grille de jeu
La grille de jeu est un hypercube en quatre dimensions de 5 cases de côté. Un hypercube est l'équivalent d'un carré en 2D ou d'un cube en 3D. Le nombre de cases de l'hypercube est de $5 \times 5 \times 5 \times 5$ soit 625 cases.
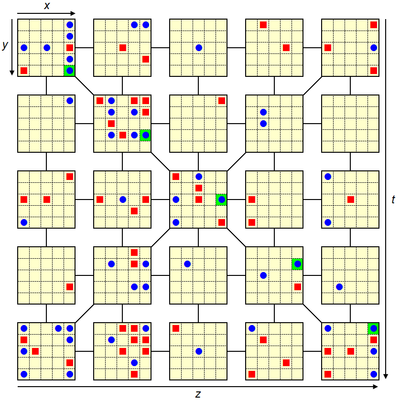
La première difficulté consiste à représenter l'hypercube sur une feuille de papier en 2D. La figure ci-dessous montre une représentation possible de l'hypercube qui va être le support du jeu. Le fichier PDF ![]() suivant (27,9 ko) contient la même grille vierge en version imprimable.
suivant (27,9 ko) contient la même grille vierge en version imprimable.
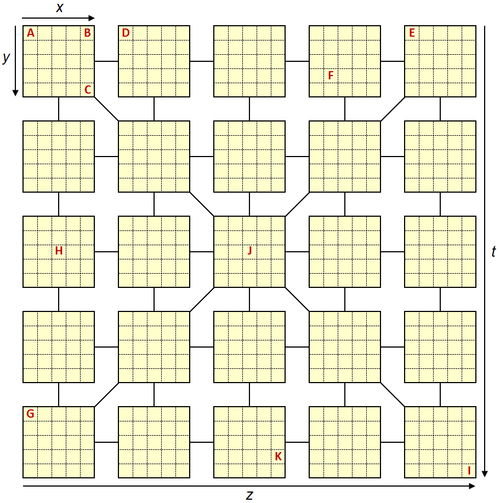
Pour comprendre comment la grille fonctionne, le plus simple est d'utiliser un repère (une origine et des axes) et de repérer chaque case par ses coordonnées. En quatre dimensions, le repère possède quatre axes: $x$, $y$, $z$ et $t$, et chaque case est représentée par quatre nombres, chacun étant la position sur un de ces axes. Quelques exemples de points ont été placés dans la figure ci-dessus:
-
La case A est choisie comme origine et a pour coordonnées (0,0,0,0).
-
Le bloc de $5 \times 5$ cases en haut à gauche est un plan parallèle à $x$ et $y$ dont tous les points ont pour coordonnée $z = 0$ et $t = 0$. Dans ce bloc les coordonnées $x$ et $y$ de chaque case se lisent comme dans un repère 2D habituel. Ainsi, les coordonnées des points B et C sont:
-
B(4,0,0,0)
-
C(4,4,0,0)
-
-
A droite du bloc de $5 \times 5$ cases décrit ci-dessus se trouvent quatre autres blocs. Ceux-ci correspondent à des plans superposés, permettant de parcourir la troisième dimension $z$. Cet ensemble de 5 blocs peut être vu comme un cube que l'on a découpé en 5 tranches et dont les tranches carrées (ayant chacune 25 cases) ont été placées les unes à côté des autres de gauche à droite. Ainsi la coordonnée $z$ augmente en passant d'un bloc à l'autre de gauche à droite. Les coordonnées des points D, E et F sont donc:
-
D(0,0,1,0), car le point est dans le deuxième bloc en partant de la gauche (donc $z = 1$) et car à l'intérieur de ce bloc les coordonnées $x$ et $y$ se lisent de la même façon que dans le premier bloc.
-
E(0,0,4,0)
-
F(1,3,3,0)
-
-
En partant du premier bloc en haut à gauche, la quatrième dimension est explorée en se déplaçant d'un bloc à l'autre non plus de gauche à droite, mais de haut en bas. Ainsi, la coordonnée $t$ varie de 0 à 4 et les points G et H ont pour coordonnées:
-
G(0,0,0,4)
-
H(2,2,0,2)
-
-
On peut combiner les déplacements d'un bloc à l'autre de gauche à droite et de haut en bas pour faire varier à la fois les coordonnées $z$ et $t$. En se déplaçant également de gauche à droite et de haut en bas au sein d'un bloc, on fait aussi varier $x$, et $y$ et les points I, J et K ont pour coordonnées:
-
I(4,4,4,4): point à l'opposé de A
-
J(2,2,2,2): centre de l'hypercube
-
K(4,3,2,4): la case est dans le troisième bloc de gauche à droite ($z = 2$) et cinquième de haut en bas ($t = 4$), et à l'intérieur du bloc $5 \times 5$, les coordonnées $x$ et $y$ valent 4 et 3 respectivement.
-
But du jeu
Le gagnant est le premier joueur qui arrive à aligner 5 pions. Les pions peuvent être alignés dans n'importe quelle dimension et même former des diagonales selon 2, 3 ou 4 des dimensions de l'hypercube. Des exemples plus bas donnent un aperçu de tous les types d'alignement possibles, qui sont au nombre de 888 (contre 8 seulement pour un morpion classique $3 \times 3$).
Déroulement du jeu
Le jeu se joue à deux et les joueurs placent un pion à tour de rôle, comme dans le jeu de morpion classique.
Exemples de pions alignés (lignes gagnantes)
Dans toutes les grilles représentées dans cette section, les pions d'une même couleur forment une ligne gagnante.
Lignes traversant une seule dimension
La dimension traversée le long de la ligne peut-être $x$, $y$, $z$ ou $t$.
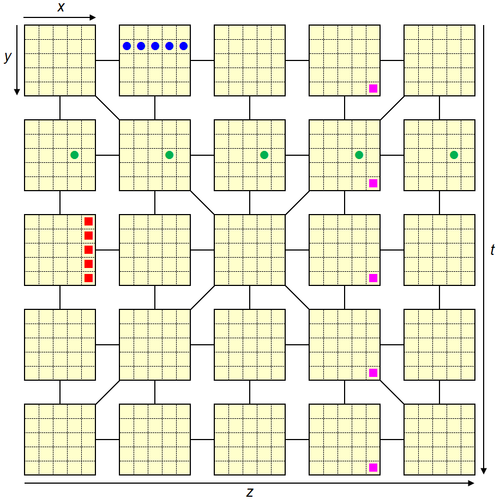
Pour les cas $x$ et $y$, c'est facile, car ce sont des lignes simples dans un des blocs de $5 \times 5$ cases de la grille (exemples des pions bleus et rouges dans la figure ci-dessous).
Les lignes selon $z$ et $t$ sont faites de 5 pions, chacun étant dans un bloc à la même position $x$ et $y$, et dont les 5 blocs hôtes sont alignés horizontalement ou verticalement dans la grille (exemples: les lignes en vert et rose respectivement ci-dessous).
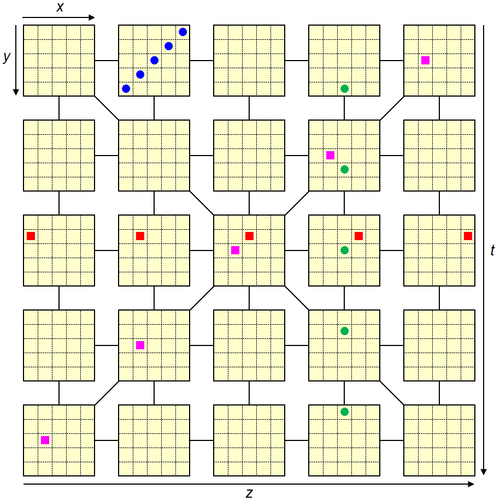
Lignes traversant deux dimensions
Lorsque les deux dimensions traversées sont $x$ et $y$, les 5 pions sont dans un unique bloc et forment une diagonale facile à voir telle qu'avec les pions bleus dans la figure ci-dessous.
Pour les pions rouges, les dimensions traversées sont $x$ et $z$. En passant d'un pion au pion voisin (de gauche à droite), on a à la fois les coordonnées $x$ et $z$ qui sont incrémentées de 1.
Il est également possible d'avoir un incrément de 1 pour une des coordonnées et de -1 pour l'autre. C'est le cas de l'alignement des pions verts, où, en parcourant les blocs de haut en bas, la coordonnée $y$ diminue de 1 d'un pion à l'autre et la coordonnée $t$ augmente de 1.
Les deux coordonnées variables peuvent être $z$ et $t$, ce qui se matérialise par 5 pions dans des blocs différents. Les blocs en question sont le long d'une grande diagonale sur la grille, mais à l'intérieur de chaque bloc, la position des pions est toujours aux mêmes coordonnées $x$ et $y$.
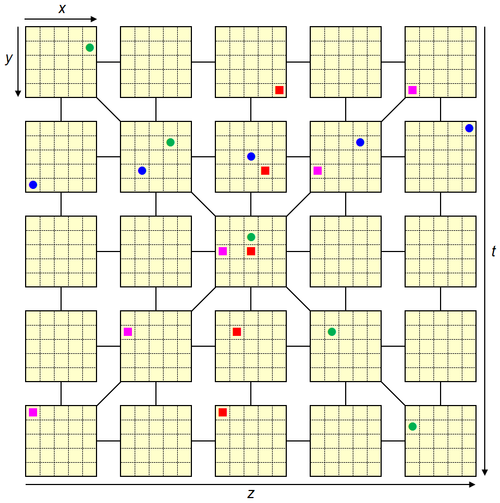
Lignes traversant trois dimensions
Ce sont les lignes les plus difficiles à visualiser. Dans les exemples ci-dessous, les coordonnées qui varient le long d'une ligne sont indiquées:
-
Pions bleus: d'un pion à l'autre, $x$ est incrémenté de 1, $y$ de -1 et $z$ de 1, en parcourant les blocs de gauche à droite.
-
Pions rouges, de haut en bas: $x$ et $y$ sont incrémentés de -1 et $z$ de 1.
-
Pions verts, de gauche à droite: $x$ est incrémenté de -1 et $z$ et $t$ sont incrémentés de 1.
-
Pions roses, de droite à gauche: $y$ et $z$ sont incrémentés de -1 d'un pion à l'autre et $t$ de 1.
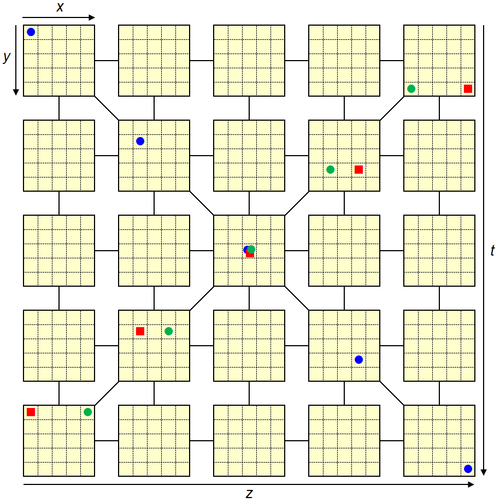
Lignes traversant les quatre dimensions
Ces lignes passent nécessairement par le centre de l'hypercube, et les quatre coordonnées varient d'un point à l'autre sur une même lignes. Bien que seulement trois diagonales soient représentées ci-dessous, il en existe huit possibles.
Programme
Il n'est pas facile au début de voir tous les coups intéressants, ni de déterminer si une ligne est gagnante ou non. Le programme suivant (au format Excel) permet de s'entrainer en jouant à deux, ou contre l'ordinateur. Dans les deux cas, l'ordinateur vérifie et indique à chaque coup si une ligne est gagnante:
Si à l'ouverture du fichier, le bouton "Nouvelle partie" ne fonctionne pas, il faut activer les macros:
-
Si un bandeau tel que celui ci-dessous s'affiche, cliquer sur Options et cocher "Activer ce contenu".

-
Sinon, cliquer sur le bouton "Sécurité des macros" dans l'onglet Développeur, choisir "Désactiver toutes les macros avec notification" et redémarrer le classeur. Le bandeau mentionné plus haut doit alors apparaitre et permettre d'activer les macros du fichier.

Autres jeux en 4D
Le morpion n'est pas le seul jeu à avoir été adapté en quatre dimensions. Parmi les plus connus, il y a le Magic Cube 4D (Rubik's cube $3 \times 3 \times 3 \times 3$) et Frac4D (équivalent 4D du Tetris).