Qu'est-ce que le mouvement brownien?

Introduction

Le mouvement brownien est le nom du phénomène correspondant au mouvement aléatoire de particules dans un fluide. Cette page fournit un bref historique de sa découverte, ainsi qu'une explication basique du phénomène.

Observation par Brown

Le mouvement brownien a été observé par le botaniste Robert Brown en 1827, dont le nom a été retenu pour nommer le phénomène. Brown observait alors des grains de pollen au microscope. Ces grains, lorsqu'ils étaient dispersés dans l'eau, éjectaient des petites particules. Celles-ci étaient alors sujettes à un mouvement aléatoire dans le liquide. Il semblait que les particules avaient un moteur pour les faire nager, ou que quelque chose dans l'eau les poussait. Brown a ensuite visualisé d'autres types de particules, certaines organiques (provenant de la vie animale ou végétale), et d'autres pas. Comme des particules inorganiques bougeaient également aléatoirement, il en a conclu que le phénomène n'avait pas une origine biologique.

Explication qualitative

Les fluides sont faits de molécules qui bougent en permanence par agitation thermique

Le mouvement brownien de particules dans un fluide provient du fait que le fluide est lui-même fait de particules (des molécules). Dans un liquide, les molécules sont proches les unes des autres mais peuvent quand même se déplacer les unes par rapport aux autres (sinon, on aurait un solide). Ces molécules sont soumises en permanence à une agitation thermique, c'est-à-dire que les particules bougent et vibrent les unes par rapport aux autres. L'agitation thermique représente le phénomène microscopique principal qui fait qu'un matériau peut stocker de la chaleur: tout ce qui est chaud, c'est-à-dire au dessus de la température du zéro absolu (-273,15 °C), stocke la chaleur sous la forme d'agitation moléculaire.

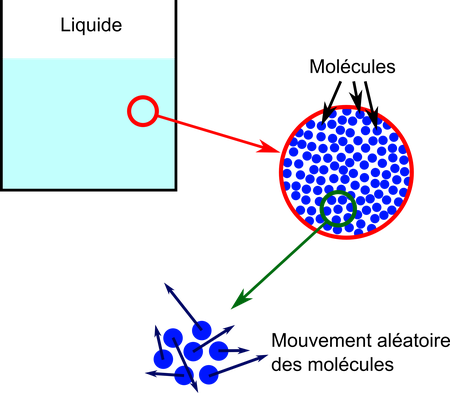
Des particules ajoutées à un fluide entrent en collision avec les molécules de manière aléatoire

Lorsque des grosses particules comme celles des grains de pollen sont insérées dans le fluide, celles-ci se retrouvent dans un bain de plein de molécules. Les molécules, qui bougent par agitation thermique, vont rentrer en collision avec les particules. À chaque collision entre une molécule et une particule, la molécule va appliquer une force sur la particule et lui transférer une certaine quantité de mouvement. Chaque collision conduit donc à une force aléatoire sur la particule, à la fois dans sa direction et son amplitude. La réaction de la particule à cette force est un petit déplacement dans une direction aléatoire. Le déplacement du à cette force n'est pas infini, car la viscosité du fluide à tendance à stopper tout déplacement de la grosse particule. La particule se déplace donc d'un "pas" d'une taille et direction et aléatoires à chaque collision avec une molécule. C'est ce phénomène qui anime les particules provenant du pollen que Brown a observées.

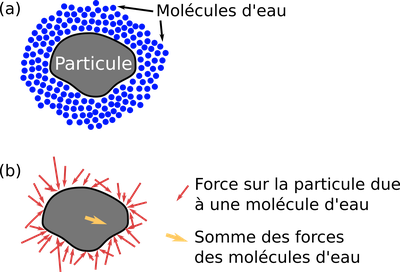
Un problème de statistiques

La description des chocs aléatoires avec les molécules permet de déduire les propriétés statistiques du mouvement des particules. En particulier:

• Le déplacement pendant un temps donné d'une particule est nul en moyenne. Bien que la particule bouge, elle a autant de chances de se déplacer à gauche ou à droite, car les collisions se produisent dans toutes les directions.

• Pour décrire l'"amplitude" du mouvement quand celui-ci a une direction moyenne nulle, il est courant de le caractériser par son déplacement quadratique moyen. C'est une quantité reliée à la mesure de la distance moyenne parcourue par une particule après un certain temps. Celle-ci n'est pas nulle en moyenne, et a les propriétés suivantes:

  • Plus les molécules tapent la particule fort et souvent, plus le déplacement quadratique moyen est grand. L'"amplitude" du mouvement Brownien augmente donc avec la température, car l'agitation thermique augmente.

  • Plus les particules sont grosses, plus l'amplitude du mouvement Brownien est faible. Quand la taille des particules augmente, leur surface augmente et les collisions avec les molécules sont plus nombreuses. Mais l'augmentation de la taille conduit également à une augmentation de la masse des particules, et un choc provoque un déplacement plus faible. La combinaison de ces deux variations conduit à un déplacement plus faible pour des grosses particules. La raison à cela est une propriété statistique appelée la loi des grands nombres. Dans le contexte du mouvement brownien, elle signifie que plus le nombre de chocs aléatoires est important, plus la moyenne de la somme des chocs sera proche de zéro. C'est pour cela que l'on ne voit pas de mouvement brownien avec des objets macroscopiques comme une balle dans une piscine. En pratique, les particules visibles au microscope ont une taille typique d'au moins un micromètre, qui est assez proche de la taille à partir de laquelle le mouvement brownien devient négligeable. Ainsi, on peut voir clairement au microscope que des gros objets ne sont pas sujets au mouvement Brownien, alors que des petits le sont.

Représentation du mouvement brownien par une marche aléatoire

Une représentation correcte et simple du mouvement brownien d'une particule au cours du temps consiste à découper le temps en petits intervalles et de supposer que pendant chaque intervalle, la particule se déplace d'un pas d'une longueur fixe mais d'une direction aléatoire. Ainsi, il est facile de simuler le mouvement brownien avec un ordinateur pour illustrer certaines de ses propriétés statistiques.

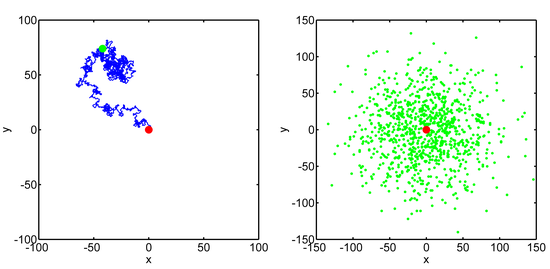
Explication par Albert Einstein

En 1905, Einstein a fourni une description quantitative du mouvement brownien. Ses prédictions ont ensuite été vérifiées expérimentalement par Jean Perrin quelques années plus tard.

Le déplacement quadratique moyen décrit ci-dessus correspond à un processus de diffusion, c'est-à-dire que si une particule est à la position $x = 0$ initialement, elle sera après un temps $t$ à une position $x$ vérifiant

$$\left< x^2 \right> = 2 D \, t$$

où $\left< x^2 \right>$ représente le déplacement quadratique moyen (les crochets indiquent de prendre la valeur moyenne de $x^2$ lorsqu'on répète l'expérience plusieurs fois), et $D$ est un coefficient de diffusion. Einstein a établi une expression du coefficient de diffusion qui vaut pour des particules sphériques de rayon $R$

$$D = \frac{k_{\text B} T}{6 \pi \, \eta R}$$

où $k_{\text B}$ est une constante (constante de Boltzmann), $T$ la température, $\eta$ la viscosité du liquide et $R$ le rayon des particules. Dans cette formule, on voit bien que le déplacement quadratique moyen augmente avec la température et diminue avec la taille des particules, en accord avec les arguments statistiques précédents. L'expression du coefficient de diffusion est particulièrement intéressante, car elle fait aussi intervenir la viscosité du liquide. $6 \pi \, \eta R$ est en fait le coefficient de friction des particules dans le liquide. Ainsi, dans le processus de diffusion, les fluctuations thermiques ($k_{\text B} T$) des molécules augmentent la diffusion, alors que la friction, qui a tendance à ralentir et stopper les particules après qu'elles subissent une force aléatoire, la diminue.

Vidéos supplémentaires de mouvement brownien

La vidéo en début de page et les deux suivantes montrent le mouvement brownien de particules dans différents systèmes: des solutions de colloïdes (microbilles de taille très régulière), et dans du lait pour lequel des globules de graisse jouent le rôle des particules. Les vidéos à température ambiante ont été obtenues avec un objectif de grandissement 60x et sont en vitesse réelle.

La comparaison des deux vidéos de microbilles de différentes tailles (1 μm dans l'introduction, et 5 μm dans cette section) montre que le déplacement aléatoire est plus important pour des petites particules que pour des grosses. Dans le cas du lait (dernière vidéo), le système est un mélange de particules de différentes tailles et leur concentration est élevée. Le mouvement brownien apparait alors comme un scintillement sur la vidéo, car beaucoup de particules de l'échantillon en 3D ne restent pas dans le plan 2D de l'image.

Pour pouvoir observer le mouvement brownien, il faut dans tous les cas un montage permettant de voir des petits objets, comme un microscope, car le mouvement est trop faible quand les particules sont trop grandes!