Diffusion de jus de citron dans du poulet

Introduction

Certaines viandes se cuisinent en marinade. Il faut alors laisser la viande plusieurs heures pour laisser le temps à la marinade de pénétrer dans la chair par diffusion. Cette expérience caractérise la diffusion de jus de citron dans un morceau de poulet et permet d'obtenir une valeur expérimentale du coefficient de diffusion.

Expérience

Principe de l'expérience

Le but de l'expérience est de placer un bout de poulet en contact avec du jus de citron et d'observer l'évolution du front de jus de citron à l'intérieur du poulet. L'intérêt du poulet est que la chair vire du rose au blanc au contact du citron, ce qui rend les mesures faciles. Typiquement, on peut caractériser la diffusion du jus en mesurant l'avancement moyen du jus de citron dans le poulet en fonction du temps. La théorie de la diffusion prédit une loi du type :

$$x^2 = D t$$

où $t$ est le temps écoulé depuis le début de l'expérience, $x$ est la position du front de jus de citron et $D$ est une constante appelée coefficient de diffusion. La constante dépend de la viande et du liquide.

Préparation de l'échantillon de poulet

Le but est de remplir un tube transparent avec un morceau de poulet. Techniquement, il est assez difficile de faire ceci dans un petit tube à essai, car des bulles d'air remontent dans le tube lorsque l'on enfonce le poulet dedans. La méthode indiquée ci-dessous résout ce problème en utilisant un tube ouvert des deux côtés :

• Si tu as des pipettes en plastique, coupes-en une à la base de la pomme pour obtenir un tube ouvert. Si tu as des pipettes Pasteur, elles sont déjà ouvertes des deux côtés.

• Découpe un morceau de poulet en forme de lanière de quelques centimètres et d'un diamètre proche du diamètre intérieur du tube.

• Il faut maintenant insérer la lanière de poulet dans le tube :

  • Coupe un morceau d'environ 40 cm de fil à coudre.

  • Attache un bout du fil à une extrémité de la lanière.

  • Fait passer l'autre bout du fil dans le tube.

  • Il suffit alors de tirer sur le fil pour faire progresser la lanière dans le tube. Essaie d'éviter la formation de poches d'air entre le poulet et les parois du tube. Tire le poulet jusqu'à ce qu'il soit au milieu du tube.

  • Bouche une extrémité du tube avec le scotch.

Lancement de l'expérience

L'expérience débute lorsque le poulet entre en contact avec le jus de citron :

• Ajoute du jus de citron par l'extrémité ouverte du tube. Note l'heure.

• Bouche l'extrémité libre du tube avec du scotch. Le dispositif devrait maintenant ressembler à ceci :

• Conserve l'échantillon verticalement dans le frigo (avec le jus de citron en haut).

• Au bout d'une demi-heure, tu devrais voir apparaitre une interface rose/blanc dans la chair. C'est cette interface qui définit le front d'avancement du poulet. Avec la règle, mesure la position de cette interface par rapport à l'interface chair/liquide. La vitesse du front diminue avec le temps. Note l'avancement du front de temps en temps dans un tableau comme celui-ci :

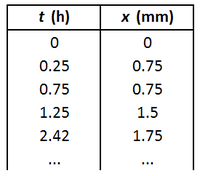
• Arrête l'expérience quand il devient trop difficile de déterminer quelle est la position du front. Typiquement, il n'est pas facile d'aller au-delà d'une semaine. De plus, plus le temps avance, plus le poulet se dégrade, et son coefficient de diffusion pourrait alors changer.

Analyse des données

Trace un graphe de l'avancement du front $x$ en fonction du temps $t$ :

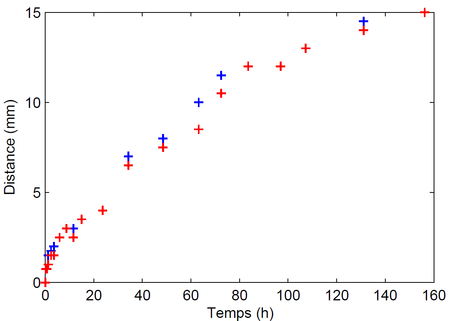
Le graphe montre qu'au début, le jus de citron s'imprègne rapidement dans le poulet (la pente est élevée aux temps courts sur la courbe) mais que la vitesse d'avancement diminue avec le temps.

Si la loi de la diffusion est valide dans cette expérience, on devrait obtenir une droite passant par zéro lorsque l'on trace le carré de la distance en fonction du temps (vois la formule indiquée plus haut).

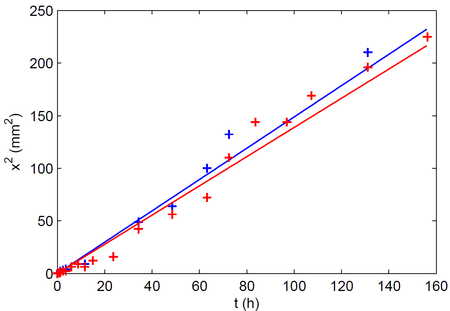
Relie les points par une droite passant par l'origine. Le coefficient de diffusion D correspond à la pente de cette droite. Dans mon expérience, j'ai trouvé que le jus diffuse comme prévu par la loi de la diffusion car on a bien des points le long d'une droite (à peu près). J'ai trouvé les coefficients de diffusion suivants :

$$\boxed{D_{\parallel} = 1.5\,\text{mm}^2\!/\text{s} \quad \text{et} \quad D_{\perp} = 1.4\,\text{mm}^2\!/\text{s}}$$

pour des fibres respectivement parallèles et perpendiculaires au tube.

Une autre manière de représenter la diffusion est de prendre une photo de l'échantillon à des temps dont le carré évolue linéairement : par exemple après 0, 4, 16, 36... heures. En plaçant les photos de l'échantillon côte-à-côte, on voit l'avancement linéaire du front en fonction de la racine carrée du temps :

Conclusion

Le jus de citron diffuse bien dans le poulet comme prédit par la loi de la diffusion : le front avance proportionnellement à la racine carrée du temps. Le front devient également moins net avec le temps, ce qui est caractéristique d'un phénomène de diffusion. Comme la diffusion fait avancer le jus de citron dans le poulet, on pourrait penser que l'orientation des fibres pourrait influencer la vitesse d'avancement. D'après l'expérience ci-dessus, cela ne semble pas être le cas : les coefficients de diffusion pour des fibres parallèles ou perpendiculaires au tube sont quasiment identiques.