Ce qu'il te faut
- Facultatif : Ciseaux
- Facultatif : Imprimante
Introduction
Cette page décrit et explique un paradoxe géométrique sur la comparaison de l'aire de deux formes. En plus de la description ci-dessous, la 
feuille à découper suivante (1,57 ko) peut être imprimée pour mieux visualiser le paradoxe.
Paradoxes des triangles
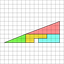
La figure ci-dessous montre deux façons d'assembler quatre formes géométriques sans les superposer. Dans le premier cas, on obtient un triangle rectangle de 13 carreaux de côté horizontalement, et 5 carreaux verticalement. Le deuxième schéma montre une deuxième manière d'assembler les quatre pièces. La deuxième forme donne aussi un triangle rectangle de 13 et 5 carreaux de côté, mais auquel il manque un carreau.
Le paradoxe est le suivant:
-
La deuxième forme est la même que la première, mais avec un carreau en moins. Son aire est donc plus petite que la première forme.
-
Mais les deux formes ont été créées en assemblant les même pièces sans superposition. Elles doivent donc avoir la même aire.
Les deux constats sont contradictoires, et ce raisonnement est faux quelque part.
Explication
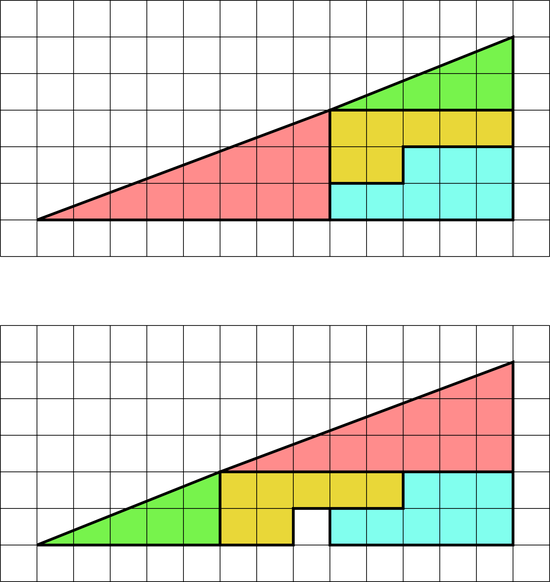
La clé du paradoxe est que les suppositions que la première forme est un triangle, et que la deuxième est un triangle moins un carreau sont fausses. La figure ci-dessous met en évidence le problème en reliant par un segment en pointillées les points B et C des supposés "triangles". L'épaisseur des traits a été réduite pour mieux mettre en évidence le problème (clique sur l'image pour l'agrandir).
Le schéma montre que sur les deux formes, le point D à la jointure des triangles vert et rouge n'est pas sur la ligne pointillée. Les segments BD et DC ne sont donc pas parallèles et ne forment pas un segment unique: La forme du haut n'est donc pas un triangle, et celle du bas n'est pas un triangle avec un carreau manquant.
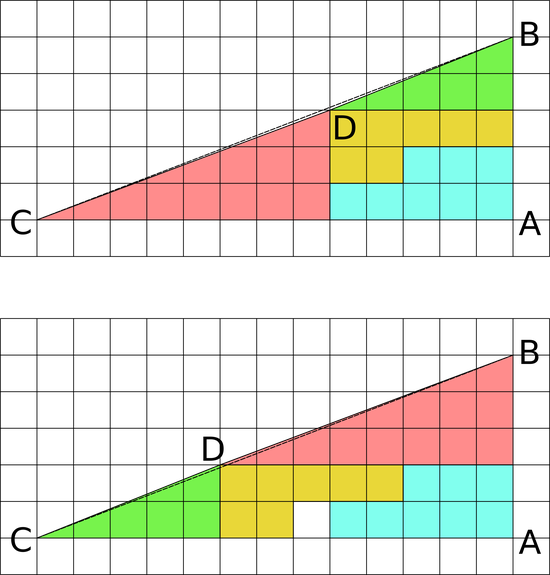
Une autre façon de voir que les segments BD et DC ne sont pas parallèles est de superposer les triangles rouge et vert:
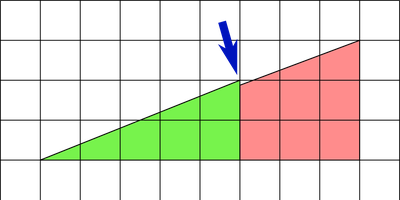
Une manière de quantifier la différence de parallélisme est de calculer, pour chacune des pièces triangulaires, la tangente de l'angle de gauche, qui est le rapport entre la taille du côté vertical et du côté horizontal. Le rapport est de 2/5 pour le triangle vert et de 3/8 pour le triangle rouge, soient 0,4 et 0,375, respectivement. La différence est minime, et donc à peine visible à l'œil nu.
Le point D étant légèrement en dessous du segment BC sur la première forme, et un peu au-dessus sur la deuxième forme, l'aire de la première forme est plus petite que celle du triangle ABC, et celle de la deuxième forme en incluant le carreau manquant est plus grande que l'aire d'ABC. En fait la différence entre ces deux formes est exactement un carreau!
Conclusion
Il n'y a en réalité pas de paradoxe. Notre œil a tendance à croire que les deux formes sont des triangles (moins un carreau pour la deuxième). C'est presque le cas, mais ce n'est pas vrai, et une observation rigoureuse des deux figures permet de mettre en évidence la différence.