Comment mesurer le coefficient de friction d'un cheveu?

Introduction

La friction est un phénomène omniprésent, qui peut être désirable ou indésirable. La friction statique, en particulier détermine les forces qu'il faut appliquer à un objet pour commencer à le déplacer sur une surface. C'est ce phénomène qui empêche par exemple de tomber sous la douche, où un coefficient de friction statique élevé est recherché. Pour pouvoir démarrer une luge facilement, il vaut mieux par contre avoir un coefficient de friction faible. La friction est aussi un paramètre important caractérisant une chevelure, car elle détermine par exemple la facilité à se peigner, ou à faire des nœuds. C'est donc un paramètre important à mesurer lors de tests de produits comme des shampoings.

Mesurer le coefficient de friction d'un cheveu est en fait très facile, et cette page explique comment le faire à la maison. Avec cette expérience, il est possible de comparer des cheveux conditionnés différemment, par exemple avant ou après shampoing.

Qu'est-ce que le coefficient de friction statique?

La quantité mesurée dans cette expérience est le coefficient de friction statique, noté $\mu_{\text s}$. Pour comprendre à quoi il correspond, considère un bloc sur une pente faisant un angle $\alpha$ avec le plan horizontal (voir figure ci-dessous). Lorsque la pente est faible, le bloc reste immobile. En augmentant l'angle $\alpha$, il va arriver un moment où le bloc commence à glisser. Cette pente critique est directement reliée à la friction statique car elle définit un seuil d'équilibre de forces à partir duquel le bloc va commencer à se déplacer.

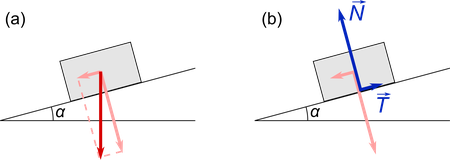
La figure (a) ci-dessus représente en rouge foncé la force gravitationnelle qui agit sur le bloc et qui a tendance à le pousser vers le bas. Cette force (un vecteur), verticale, peut être écrite comme la somme de deux composantes: l'une dans la direction de la pente, et l'autre dans la direction orthogonale (flèches en rouge clair en (a)). Pour un angle faible pour lequel le bloc ne glisse pas, cette force doit exactement compenser d'autres forces, car d'après la première loi de Newton, la somme des forces agissant sur bloc doit être nulle. Ces autres forces sont celles de la réaction de la surface en pente sur le bloc. De la même façon que la force de gravitation, elles peuvent être écrites avec deux composantes, dans les directions parallèle et orthogonale au plan en pente (flèches $\overrightarrow T$ et $\overrightarrow N$, respectivement, en bleu foncé en (b)). La force $\overrightarrow T$ correspond à la force de friction. En raison de l'équilibre, les forces de réaction en bleu ont la même amplitude (taille) que les forces de gravitation décomposées comme indiqué précédemment. C'est pour cela que cette configuration de bloc sur une pente est directement en lien avec la friction.

Lorsque l'angle $\alpha$ est augmenté, le seuil à partir duquel le bloc commence à glisser définit le coefficient de friction statique comme le ratio entre les amplitudes des forces $\overrightarrow T$ et $\overrightarrow N$:

$$\mu_{\text s} = \frac{T}{N}$$

$T$ et $N$ ne dépendent pas eux-même du coefficient de friction, mais seulement de $\alpha$: quand $\alpha$ augmente, $T$ augmente et $N$ diminue, donc le rapport $T\!/N$ augmente, jusqu'à atteindre $\mu_{\text s}$. Ainsi, plus $\mu_{\text s}$ est grand, plus il faudra une pente élevée pour que le bloc glisse. C'est ce seuil d'équilibre de forces qui va être mesuré dans cette expérience pour un cheveu en contact avec lui-même. Dans ce cas, le cheveu joue à la fois le rôle du bloc et de la surface en pente.

Expérience

Prends quelques cheveux de ton choix (au moins 5 cm de long): par exemple, pour une même personne, quelques-uns coupés juste après un shampoing, d'autres après application d'un après-shampoing, et enfin d'autres d'une chevelure "sale". Tu peux aussi comparer des brins de différentes personnes. Pour chaque cheveu, l'expérience est en deux étapes: d'abord une mesure de son diamètre, puis une mesure de la taille d'un nœud. (Si ce n'est pas clair à ce stade en quoi tout cela est relié à la friction, c'est normal; les explications sont plus bas!)

Mesure du diamètre d'un cheveu

Mesure le diamètre du cheveu par diffraction laser en suivant les instructions sur cette page: Mesurer l'épaisseur d'un cheveu par diffraction laser. Le diamètre est noté $d$.

Mesure du coefficient de friction statique

Pour obtenir le coefficient de friction statique, il faut mettre le cheveu dans une configuration dans laquelle il se touche lui-même et dans laquelle le système est "tendu", c'est-à-dire à la limite de voir le cheveu glisser contre lui-même. Cette condition qui semble au premier abord complexe à réaliser expérimentalement est en fait facile à satisfaire.

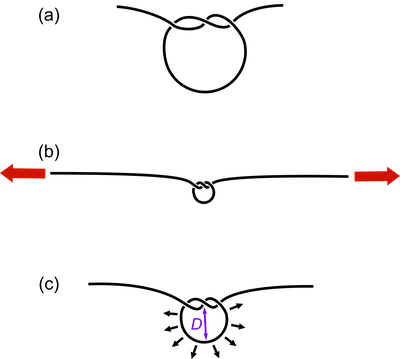
Comme indiqué sur le schéma ci-dessus, suis les étapes suivantes:

• (a) Fais un nœud simple avec le cheveu.

• (b) Tire doucement les extrémités du cheveu pour serrer le nœud. Attention, le nœud ne doit pas être serré entièrement, car il ne faut pas qu'il subisse de déformations irréversibles. Typiquement, serrer le nœud jusqu'à un diamètre de 1 ou 2 mm devrait aller.

• (c) Relâche les extrémités. Le nœud doit alors se desserrer tout seul jusqu'à atteindre un certain diamètre. Si le nœud ne se desserre pas, reprends l'étape précédente en serrant légèrement plus.

La dernière étape est celle qui relie l'expérience à la friction. Le cheveu préfère être droit plutôt que courbé au sein d'un nœud, ce qui se caractérise par une élasticité de courbure du cheveu qui a tendance desserrer le nœud. Lorsque la courbure est élevée (nœud serré), la force qui veut desserrer le nœud est suffisamment grande pour qu'au contact du cheveu avec lui-même il y ait glissement. Quand le nœud s'agrandit, cette force diminue et atteint à un moment le seuil en-dessous duquel il n'y a plus de glissement. Lorsque le nœud se desserre en se frottant contre lui-même, puis s'arrête à une forme en équilibre, celle-ci permet de déterminer le coefficient de friction statique, comme dans l'expérience du bloc sur une pente au seuil de glissement. Alors que pour le bloc sur une pente il fallait augmenter l'angle pour changer les forces de friction $T$ et $N$ et atteindre le seuil de glissement, lorsque le nœud se desserre, les forces de frictions varient ici de manière à ce que le rapport $T\!/N$ diminue jusqu'à atteindre le seuil de non-glissement. Ceci se produit pour un certain diamètre d'équilibre du nœud, qui permet de déduire le coefficient de friction.

• Mesure le diamètre du nœud après qu'il se soit desserré spontanément. Note cette valeur $D$.

• Calcule le coefficient de friction en utilisant la formule suivante, qui provient d'un calcul formalisant le phénomène décrit ci-dessus:

  $$\mu_{\text s} = \text{1,02} \, \sqrt{\frac{d}{D}}$$

$\mu_{\text s}$ est un nombre sans dimension. Tu devrais trouver typiquement une valeur entre 0,1 et 0,2.

Test de plusieurs types de cheveux

L'intérêt de cette expérience est de comparer des échantillons de cheveux différents. Par exemple, tu peux tester des cheveux de différentes personnes, ou pour une même personne comparer des cheveux avant et après shampoing. Pour obtenir des valeurs suffisamment précises des coefficients de friction dans chaque cas, il faut faire les mesures avec plusieurs cheveux du même type, puis calculer leur coefficient de friction moyen.

Le tableau ci-dessous récapitule des mesures sur deux types de cheveux d'une même personne (moi): cheveux secs juste après un shampoing (type A) et cheveux secs trois jours après le dernier shampoing (type B).

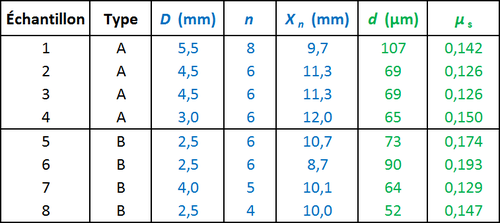
Dans ce tableau, les nombres en bleu sont des mesures et les nombres en vert des résultats d'un calcul utilisant ces mesures. Pour la mesure du diamètre $d$ des cheveux, la méthode 2 de la page sur la mesure de diamètre par diffraction a été utilisée (voir cette page pour la définition de $n$ et $X_n$, ainsi que pour la formule pour $d$).

D'après les mesures ci-dessus, le coefficient de friction moyen est de 0,136 pour le type A (juste après shampoing) et 0,161 pour le type B (trois jours après shampoing). C'est un résultat assez surprenant, car le rôle principal d'un shampoing est d'enlever une accumulation de graisses (sébum) dans les cheveux qui a tendance à diminuer le coefficient de friction. Ici, l'expérience montre une augmentation du coefficient de friction. Une possibilité est que les formulations des shampoings modernes sont complexes, et, en plus d'enlever la graisse des cheveux, ceux-ci peuvent contenir des composés comme des silicones qui vont justement restaurer une certaine allure un peu huileuse et éviter un effet de "cheveux secs". Selon les shampoings (marques, pour "cheveux gras" ou "cheveux secs", etc), l'effet sur le coefficient de friction peut donc être très différent.

Conclusion

Mesurer un coefficient de friction par une expérience du type "bloc sur une pente" est difficile pour de très petits objets. Pour le cas de filaments comme des cheveux, il existe cependant une méthode astucieuse qui ne requiert pas de montage complexe. La méthode du nœud simple est en fait suffisamment facile pour pouvoir être réalisée chez soi. De telles mesures montrent alors une variation du coefficient de friction en fonction du conditionnement des cheveux, ce qui peut fournir une manière de classifier des shampoings et des après-shampoing.

Références

• Hair-on-hair static friction coefficient can be determined by tying a knot, N.R. Chevalier, Colloids and Surfaces B: Biointerfaces 159, 924–928 (2017)

• Hair Cosmetics: An Overview, Maria Fernanda Reis Gavazzoni Dias, Int. J. Trichology 7(1), 2-15 (2015)