Comment varie la température d'ébullition de l'eau avec l'altitude ?

Introduction

On apprend souvent que l'eau bout à 100 °C. Mais ce n'est pas toujours vrai. En fait, c'est même le plus souvent faux, car la température d'ébullition montre une forte dépendance avec l'altitude, dont l'origine est expliquée ici.

Table de données

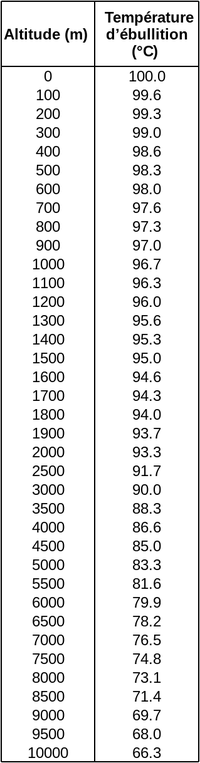
Avant des explications, le tableau ci-dessous montre la température d'ébullition de l'eau pure en fonction de l'altitude mesurée par rapport au niveau de la mer. Quand l'altitude augmente, l'eau bout à une température plus faible. Elle ne bout à 100 °C qu'au niveau de la mer (altitude: 0 mètres).

Quelques exemples:

• Chamonix se situe à 1035 mètres d'altitude en moyenne et l'eau bout à 97 °C.

• En haut du Mont Blanc, l'altitude est de 4810 m (cette valeur fluctue un peu en fonction des saisons et des années, la calotte de glace au sommet changeant d'épaisseur au gré des saisons et des années). Il faut là-haut chauffer l'eau à 84 °C pour la faire bouillir.

• La température d'ébullition descend même jusqu'à 70 °C au sommet de la montagne la plus haute sur Terre: le Mont Everest, à 8848 m d'altitude.

Origine de la variation de la température d'ébullition de l'eau

Ce n'est pas directement l'altitude qui affecte la température d'ébullition, mais la pression atmosphérique. Or celle-ci varie avec l'altitude. L'explication va donc se faire en deux étapes pour comprendre les observations suivantes:

• Quand l'altitude augmente, la pression atmosphérique diminue.

• Quand la pression diminue, l'eau bout à une température plus faible.

Changement de la pression atmosphérique avec l'altitude

La pression atmosphérique est une quantité qui représente combien l'air qui nous entoure appuie sur nous-mêmes et tous les objets autour de nous. Comme l'air appuie sur tous les côtés (y compris des côtés opposés), on ne sent généralement pas cette force, mais elle existe bien. L'origine de cette force est la gravité. La gravité terrestre attire toutes les masses vers le centre de la Terre. Or, l'air a une masse et il est donc lui aussi attiré par la Terre. Ainsi, la Terre peut avoir une atmosphère qui ne s'évade pas dans l'espace grâce à la gravité.

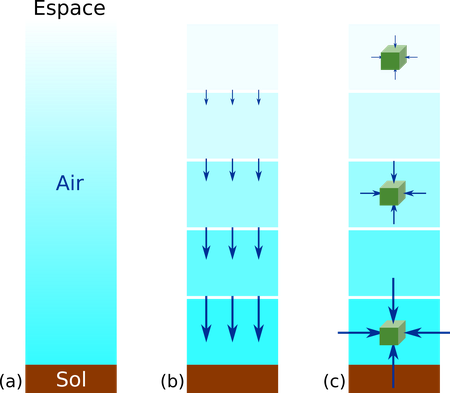
Pour comprendre comment l'air appuie différemment sur les objets autour de nous selon l'altitude, on peut considérer une colonne d'air allant du sol jusqu'à l'espace (la colonne s'arrête quand il n'y a plus d'air) comme sur le schéma (a) ci-dessous. Cette colonne peut être découpée en plusieurs blocs d'air, empilés les uns sur les autres et à des altitudes différentes (voir (b)). Pour chaque bloc, la pression de l'air du bloc peut être différente, et donc aussi la densité de l'air, les deux étant reliés (par une équation appellée l'équation du gaz parfait). La pression est déterminée pour un bloc donné en calculant combien le bloc juste au-dessus appuie sur l'air du bloc considéré (flèches bleues). Plus il y a d'air au-dessus du bloc, et plus cet air est dense (et donc à une pression élevée), plus il appuie (car attiré par la gravité) et génère une pression élevée sur le bloc. Comme les blocs près dur sol ont une colonne d'air qui les surmonte plus massive que les blocs élevés, la pression est plus grande près du sol que près de l'espace. La pression diminue donc quand l'altitude augmente. Alors que dans ce raisonnement on a considéré l'air qui appuie sur lui-même, la pression agit sur tous les objets, comme indiqué en (c) où les cubes représentent de tels objets. En particulier l'air appuiera moins sur l'eau liquide dans une casserole quand on monte en altitude.

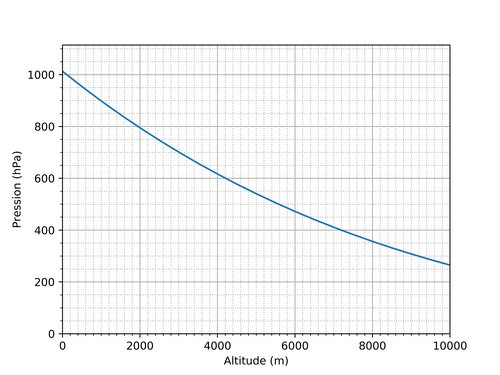
Le calcul détaillé de la pression en fonction de l'altitude est assez complexe. La première difficulté est qu'avec le raisonnement de découpage de la colonne d'air en blocs, le calcul devient un calcul différentiel (avec des intégrales). Ensuite, si on prend des blocs de volume constants, la masse d'air dans chaque bloc dépend elle-même de la densité, et donc de la pression qu'on cherche à calculer. Enfin, en fonction de la précision souhaitée, il faut éventuellement aussi prendre en compte les variations de température en fonction de l'altitude (qui affectent la densité ou la masse de l'air en fonction de la pression), ou même celles de la gravité en fonction de l'altitude. Le tableau de données sur cette page prend en compte tous ces effets et utilise un modèle de l'atmosphère moyen sec appelé le "U.S. Standard Atmosphere" établi en 1976. Le graphe ci-dessous montre la pression en fonction de l'altitude d'après ce modèle:

Changement de la température d'ébullition de l'eau avec la pression

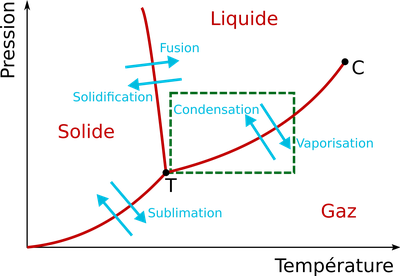
La façon dont la température d'ébullition dépend de la pression est une propriété intrinsèque de l'eau et s'obtient à partir du diagramme de phase de l'eau. Une version schématique du diagramme de phase est dessinée ci-dessous. Ce diagramme possède deux axes: la pression et la température. Pour une pression et une température quelconques, on obtient un point sur le diagramme qui est dans une zone (en général pas sur une des ligne rouge), parmi "solide", "liquide" ou "gaz", qui indique dans quel état se trouverait l'eau dans ces conditions de pression et température. Les lignes rouges indiquent les frontières entre les différents états, c'est-à-dire les conditions de température et de pression pour lesquelles l'eau peut être en train de changer d'état. Comme ce qui nous intéresse est l'ébullition, il faut regarder la courbe rouge entre la zone liquide et gaz (encadrée en pointillés verts). Cette ligne indique pour une pression donnée quelle sera la température d'ébullition de l'eau. Comme cette ligne n'est pas verticale, cela signifie que la température d'ébullition dépend de la pression.

Alors que le diagramme ci-dessus est schématique, le graphe ci-dessous indique la forme réelle de la courbe entre les zones "liquide" et "gaz" (attention: les axes de température et de pression sont inversés par rapport au schéma précédent):

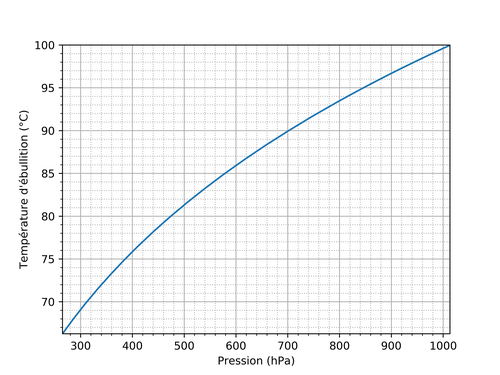
Par exemple, au niveau de la mer, la pression atmosphérique moyenne est de 1013 hPa, et on retrouve d'après cette courbe que la température d'ébullition est alors de 100 °C.

Conclusion

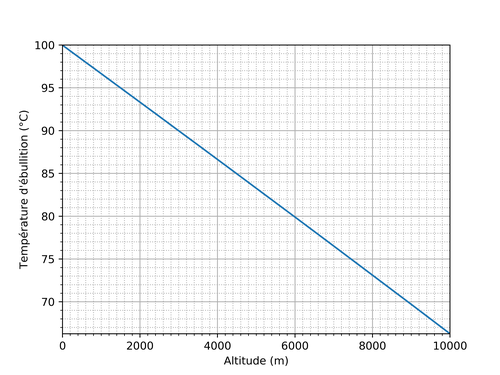
En combinant les deux courbes précédentes, c'est-à-dire en calculant pour chaque altitude la pression, puis pour les pressions obtenues, la température d'ébullition de l'eau, on obtient la relation entre la température d'ébullition et l'altitude. Le tableau en début de page peut aussi être représenté sous forme graphique, ce qui donne presque une droite:

Références

Les données de cette page utilisent:

• Le modèle "US Standard Atmosphere" tel qu'explicité dans CRC Handbook of Chemistry and Physics Data, 90e édition, David R. Lide (2010)

• La courbe de saturation de l'eau pure selon le NIST Chemistry WebBook, SRD 69