Le problème
En cuisine, certaines recettes nécessitent de faire mariner une viande avant de la cuire. Imagine la situation suivante. Il est 13 h et tu as des invités à diner. Tu as prévu du poulet au citron. Mais quel malheur ! La recette indique de faire mariner le poulet pendant 24 heures, et tu as oublié de préparer la marinade hier soir ! Il ne te reste que quelques heures avant que tes invités n'arrivent. Comment peux-tu rattraper le coup et diminuer le temps requis pour faire mariner la viande ?
Une idée de solution
Faire mariner une viande consiste à faire rentrer un jus dans la chair par simple contact avec le jus. C'est un processus lent, appelé diffusion. A l'issue du processus, chaque morceau de viande aura une surface imbibée de citron sur une certaine épaisseur, et le cœur du morceau intact. Plus la viande est marinée longtemps, plus l'épaisseur de la couche imbibée est grande. Pour réussir la recette, il faut atteindre la bonne proportion de viande non citronnée (cœur) et de viande citronnée (couche).
Comment atteindre la fraction de viande citronnée voulue, en un temps plus court que celui indiqué dans la recette ? Une solution pourrait être d'augmenter la vitesse à laquelle le front citronné pénètre dans un morceau de poulet, mais ce n'est pas faisable facilement. Pour s'en sortir, l'idée est d'augmenter la surface de poulet en contact avec le jus par rapport à ce qui est suggéré par la recette, ce qui va augmenter le volume de poulet citronné pour un temps de marinade constant, ou de manière équivalente diminuer le temps de marinade requis pour obtenir le volume de poulet citronné requis par la recette.
Résolution du problème
Le système
Raisonne sur un seul morceau de poulet. On va supposer qu'il est sphérique. La recette indique de découper des morceaux d'une taille (rayon) $r_0$ et de les faire mariner pendant un temps $t_0$. Le résultat est un morceau sphérique dont on suppose qu'il a toujours un rayon de $r_0$ (en réalité il grossit un tout petit peu), et qui possède une couche citronnée sur une épaisseur $x_0$ :
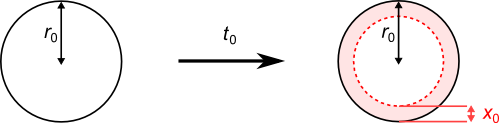
Ton objectif est d'obtenir le même pourcentage (en volume) de viande citronnée que dans la recette, mais en coupant des morceaux plus petits, de taille $r_1$, ce qui permet de mariner pendant un temps $t_1$ plus petit que $t_0$ :
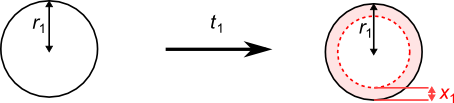
Résolution
Pour résoudre le problème, il faut inclure une équation qui provient de la physique et qui décrit l'avancement d'un front par diffusion. Dans ce problème, en supposant $x_0$ très petit devant $r_0$, la loi relie simplement l'avancement $x_0$ à la durée de marinade $t_0$ par la formule :
$$x_0^2 = D \, t_0$$Ici, $D$ est une constante appelée coefficient de diffusion, qui dépend du type de viande (ici, poulet) et du type de jus (citron). Le problème est que cette constante est inconnue (à moins de faire l'expérience de diffusion de jus de citron dans le poulet).
On peut également écrire la même équation dans le système mariné un temps court :
$$x_1^2 = D \, t_1$$En divisant la deuxième équation par la première, et en prenant la racine carrée, on obtient une relation entre $x_0$, $x_1$, $t_0$ et $t_1$ qui ne dépend pas de l'inconnue $D$ :
$$\frac{x_1}{x_0} = \sqrt{\frac{t_1}{t_0}} \quad \quad (1)$$Maintenant, il faut utiliser le fait que l'on veuille la même fraction de viande citronnée $f_0$ dans le résultat de la recette et dans le résultat en temps réduit. Dans la recette, cette fraction est définie et se calcule ainsi :
$$f_0 = \frac{V_{\text{citronné}}}{V_{\text{total}}}$$C'est donc le ratio du volume de la couronne d'épaisseur $x_0$ par le volume de la sphère de rayon $r_0$. En utilisant la formule du volume d'une sphère :
$$f_0 = \frac{\frac{4}{3} \pi r_0^3 - \frac{4}{3} \pi (r_0-x_0)^3}{\frac{4}{3} \pi r_0^3} = 1 - \left( 1 - \frac{x_0}{r_0} \right)^3 \approx \frac{3 x_0}{r_0}$$Dans la dernière étape de la ligne précédente, on a supposé que $x_0$ est très petit devant $r_0$.
De même, dans le poulet mariné en temps réduit :
$$f_1 \approx \frac{3 x_1}{r_1}$$Mais on veut $f_1 = f_0$, donc les deux équations précédentes se combinent pour donner :
$$\frac{x_1}{x_0} \approx \frac{r_1}{r_0} \quad \quad (2)$$En égalisant les équations (1) et (2) et en multipliant par $r_0$, on obtient la taille des morceaux à découper $r_1$ en fonction des autres paramètres :
$$\boxed{r_1 \approx r_0 \sqrt{\frac{t_1}{t_0}}}$$Exemple
Dans l'exemple donné dans l'introduction, $t_0 = 24\,\text h$ et $t_1 = 6\,\text h$. Il faut alors couper des morceaux de taille $r_1$ deux fois plus petits que la taille $r_0$ indiquée dans la recette.