Introduction
Cette page explique le fonctionnement de deux moteurs homopolaires faciles à réaliser chez soi (voir l'expérience correspondante). Elle explique à la fois l'origine de la force qui fait tourner le moteur et comment prédire le sens de rotation.

Moteur homopolaire avec fil libre
Description du montage
Dans ce moteur, l'aimant est fixe et posé sur une table. La pile est rajoutée par dessus et un fil d'une forme adaptée crée une boucle de courant en reliant le pôle du haut de la pile avec l'aimant. Comme le fil est simplement posé sur la pile, il est libre de tourner, et lorsqu'il est bien en contact avec la pile et l'aimant, il tourne spontanément: le montage est un moteur.
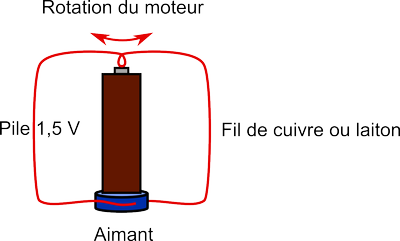
Le fil peut tourner dans le sens ou dans le sens inverse des aiguilles d'une montre. Si tu as fait l'expérience, tu as vu que le sens dépend de l'orientation de la pile et de l'orientation de l'aimant. Pour comprendre le sens de rotation, il est donc important de préciser à quel endroit la borne $+$ de la pile est branchée et où sont les pôles nord et sud de l'aimant.
Champ magnétique créé par un aimant cylindrique
Un aimant crée un champ magnétique dans l'espace. C'est celui-ci qui est responsable de l'interaction entre deux aimants par exemple. C'est un champ invisible, mais qui peut être représenté par des lignes de champ qui sortent d'un point de l'aimant, décrivent une courbe et rentrent en un autre point de l'aimant. Les lignes de champ se poursuivent également à l'intérieur de l'aimant et forment des boucles fermées. Les lignes de champ ont une orientation et le pôle nord de l'aimant est défini comme la face par laquelle les lignes de champ sortent de l'aimant tandis que le pôle sud a des lignes de champ rentrantes:
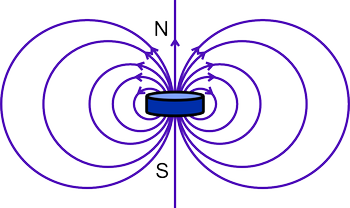
Pour déterminer les pôles nord et sud d'un aimant, tu peux pendre l'aimant à l'horizontale et l'accrocher à un fil de manière à ce qu'il puisse tourner librement sur lui-même. Le pôle nord est la face qui va alors pointer vers le nord terrestre.
Lignes de champ dans le moteur homopolaire à fil libre
On va prendre ici le cas où l'aimant est orienté avec le nord vers le haut et où la pile est collée à l'aimant par la borne moins (sur le pôle nord). Le fil métallique est alors immergé dans le champ magnétique de l'aimant (le schéma néglige la déformation du champ magnétique due à la pile):
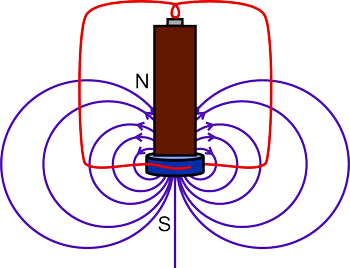
La force motrice est la force de Lorentz qui agit sur les électrons en mouvement
Comme le fil tourne spontanément (en combattant la friction), une force motrice agit sur celui-ci. La force qui fait tourner le fil sur lui-même n'existe que si l'aimant est présent et si le fil crée un circuit électrique fermé avec la pile. En fermant le circuit, la pile met des charges du fil conducteur en mouvement. Ce sont des électrons (donc chargés négativement). Ces électrons se déplacent à une certaine vitesse moyenne $v$ dans le fil, de la borne moins vers la borne plus de la pile. Or, des électrons en mouvement sont sensibles à la présence d'un champ magnétique et peuvent être ainsi déviés de leur trajectoire en raison d'une force appelée force de Lorentz. La force subie par un électron s'écrit de manière un peu compliquée avec des vecteurs:
$$F = -e \, \vec v \times \vec B$$où $-e$ est la charge de l'électron, $\vec v$ son vecteur vitesse, $\vec B$ le champ magnétique du à l'aimant à l'endroit où se trouve l'électron et $\vec F$ la force résultante sur l'électron. $\times$ est l'opérateur de produit vectoriel. Par les propriétés du produit vectoriel, la direction de $\vec F$ est orthogonale à la fois à $\vec v$ et $\vec B$ et le sens est déterminé par la règle de la main gauche expliqué ci-dessous. (Pour le produit vectoriel il faut utiliser la règle de la main droite, mais comme la formule de Lorentz pour un électron a un signe moins, ça devient la règle de la main gauche.)
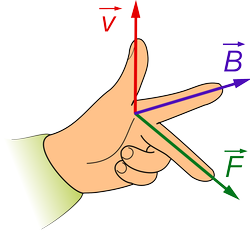
Sur le schéma du moteur homopolaire incluant les lignes de champ (section précédente), les électrons se déplacent dans le fil conducteur vers la borne + de la pile. Cela donne la direction du vecteur vitesse $\vec v$. La direction du champ magnétique $\vec B$ se lit sur le schéma en suivant les lignes de champ (en violet) et la règle de la main gauche donne alors la direction de la force agissant sur les électrons, et donc sur le fil (car les électrons sont confinés dans le fil). En prenant par exemple les portions de fil qui sont horizontales et à proximité de l'aimant, les directions des trois vecteurs sont les suivantes (pour le cas où le nord de l'aimant et le pôle $+$ de la pile sont vers le haut):
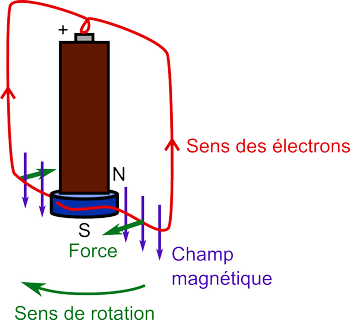
Les deux portions de fil considérées font tourner le fil dans le sens des aiguilles d'une montre. En prenant les autres portions de fil (verticales, et horizontales près de la pile), on trouve un sens de rotation identique. C'est l'ensemble de toutes ces rotations induites par la force de Lorentz sur chaque portion de fil qui conduit à la rotation rapide du fil autour de la pile. (Pour être précis, c'est la somme des couples qu'il faut considérer.)
Moteur homopolaire avec aimant libre
Dans la version ci-dessous du moteur, l'aimant est accroché à un clou qui est lui-même suspendu à la pile (le clou tient à la pile car il est magnétisé par l'aimant).
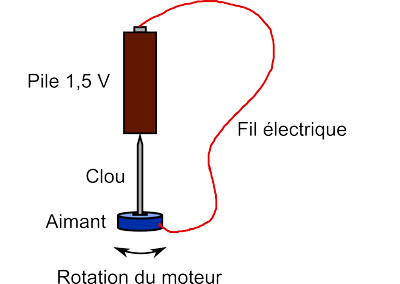
Lorsque le fil est relié à la borne du haut de la pile et à un côté de l'aimant, l'aimant et le clou se mettent à tourner. Des électrons circulent dans le fil fixe, passent par l'aimant et par le clou, qui sont tous les deux conducteurs.
Dans cette configuration, la partie du montage qui conduit à une force est principalement l'aimant, dans lequel le champ magnétique est très intense. Le détail de ce qu'il se passe à l'intérieur de l'aimant est un peu complexe. Pour obtenir le sens de rotation, il suffit cependant de supposer que les électrons se déplacent en ligne droite entre les deux points de contact, aux niveaux du clou et du fil. En supposant que l'aimant pointe son nord vers le clou et que c'est la borne $-$ de la pile qui est branchée sur le clou, les électrons vont de l'axe de l'aimant vers le bord, comme indiqué ci-dessous:
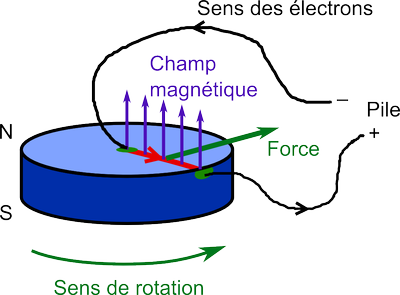
La règle de la main gauche donne alors une force sur les électrons de la portion rouge dans la direction de la flèche verte. Cette force est transmise au reste de l'aimant, conduisant à une rotation dans le sens inverse des aiguilles d'une montre.